Mind your Ps and Qs
Bill Elim
DIberikan sebuah file yang isinya sebagai berikut
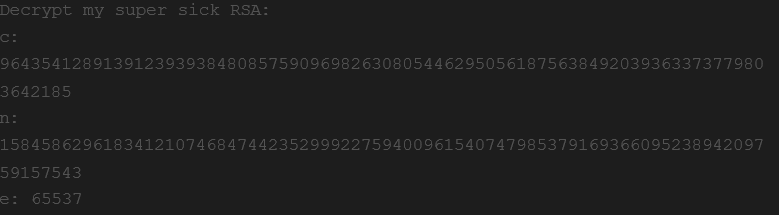
Ini adalah skema RSA sederhana, bagi yang belum tau RSA kira-kira sistemnya sebagai berikut:
Tentukan
dua bilangan prima p dan q.
Hitung n = pq
Hitung phi = (p-1)(q-1)
Tentukan e, e
biasanya bernilai antara 3 hingga 65537
Tentukan d sebagai modular multiplicative inverse
dari e modulo phi, artinya, cari
d dimana e*d % phi = 1
Untuk mengenkripsi pesan
M, lakukan:
C = M^e% n
Untuk mendekripsi ciphertext C, lakukan:
M = C^d %
n
(n,e) adalah kunci publik sedangkan (n,d) adalah kunci privat. Value yang lain
perlu dirahasiakan karena dapat digunakan untuk menghitung d.
Pada soal ini kita
diberikan kunci publik dan ciphertext untuk didekripsi, tetapi kita tidak memiliki kunci privat
sehingga kita tidak dapat langsung mendekripsinya.
Jadi, bagaimana cara merecover d hanya
dari n dan e?
Jika dilihat-lihat kita hanya perlu p dan q untuk menghitung phi dan
menggunakan phi dan e untuk mendapatkan d, jadi, cara yang bisa lakukan adalah dengan menemukan
p dan q melalui pemfaktoran n. Sayangnya n disini terlalu besar untuk di bruteforce faktornya.
jadi kita harus mencari alternatif lain.
Ada database yang sangat bagus yang
menyimpan faktor-faktor dari sebuah angka, termasuk bilangan yang cukup besar sekalipun. Yaitu
factordb, saat kita memasukkan
n yang ada di soal, maka akan keluar faktornya yaitu p dan q
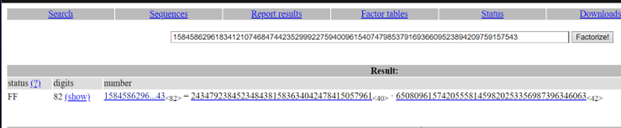
Didapatkan p = 2434792384523484381583634042478415057961 dan q =
650809615742055581459820253356987396346063
Setelah mendapatkan p dan q maka kita bisa
merekonstruksi d dan mendekripsi flagnya
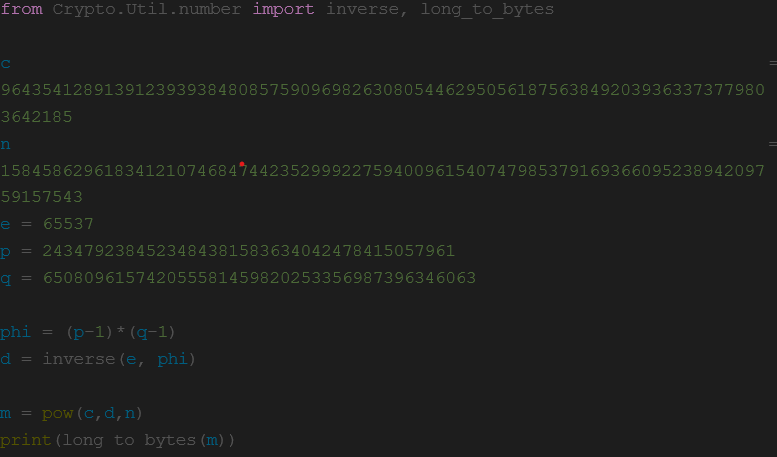

Flag: picoCTF{sma11_N_n0_g0od_73918962}